
Here are a collection of mathematical expression evaluators for double precision real and complex numeric types. Recursive descent and other techniques are combined with operator precedence rules to create evaluators which are efficient, stable and flexible. Several of the applications found elsewhere use these parsers.
An expression evaluator supporting a large set of math functions is available here. The archive includes C source code for the evaluator, a Borland static library of math functions and a driver program which demonstrates the capabilities and features of the evaluator. Variables can be created and assigned values which can then be included in subsequent expressions. The file, 'evald.c', can be edited to change the supported functions if desired. It can also be extended via external files to include user defined and written math functions. Some of the functions included in the archive were from Moshier's Cephes library.
Similar to Evald, this parser has been extended to support C++ complex double precision numeric types. The archive includes a number of complex functions from the Cephes library and from the Amos library of Bessel functions. The Amos library was created from the original FORTRAN code after translation by the Borland compatible version of F2C.
This zip archive contains source code for a parser which evaluates extended precision expressions using the XBCD_Math package. It also includes a DOS command line interpreter, a library of extended precision functions and a batch file for compiling and linking the files. Note that this application is written to compile with the Borland 32-bit compilers. A DLL version of the library which is usable from other platforms is available elsewhere on this web site.
There are many strategies for converting an ASCII text math expression into a form which can be numerically evaluated at run time. Typically, the codes are designed to accommodate constants, variables, math operators and functions. The parser/evaluator codes described in previous sections use recursive descent and operator precedence rules to solve the problem. For them, the parsing and evaluation are done (roughly) as parallel operations with the result available on completion.
For some applications, however, there is a distinct benefit gained by separating the parsing and evaluation stages so that the expression can be parsed once and subsequent evaluations of the expression can be done on a tokenized or compiled representation with different values of the expression variables. Common applications which favor this technique are function plotters, numerical integrators, iterative equation solvers and table generators.
In this archive you will find a demo program and a portable (native Pentium code) DLL containing an experimental, high performance math expression evaluator which is optimal or nearly optimal in execution time. The strategy used is to separate the parser/compiler phase from the evaluation phase and to compile the expression evaluator into native machine code with numerous optimizations. No intermediate code or tokenized representations of the expression are used. The parser/compiler uses a shift-reduce method rather than recursive descent. The resulting code actually outperforms most compiler generated code for the following reasons:
Access to the Pentium FPU is direct and highly optimized,
No stack frames are used,
Unnecessary data loads, stores and numeric type conversions are eliminated,
Constant folding and strength reduction are employed,
Functions whose arguments reduce to constants are also reduced to constants,
FPU stack monitoring is used to control stack depth during parsing,
Simple functions are directly inserted into the evaluation code without function call overhead.
The numeric data type used by this version is the IEEE 8-byte double precision type commonly used by Intel processors in general and the Pentium class processors in particular. CAUTION: The evaluation code produced by the parser/compiler is a Pentium compatible executable code string and will not work on other processor platforms.
The significant features and capabilities of this expression evaluator are:
Highly optimized native code compilation,
Support for run time addition of user defined constants and variables,
Support for run time addition of user supplied external functions.
The standard operators +, -, *, /, and ^ are supported and, as a convenience, the bang operator (!) for factorials is also supported. It has been generalized to work with real numbers so that for any x, we have: x! = G(x+1).
The included demo represents a proof of concept rather than a finished application. It barely rises to the level of a beta distribution for reasons which will be explained later. Nevertheless, and in spite of these limitations, it exhibits many of the features expected of a high performance expression evaluator and makes the internal form of the compiled solution visible for inspection.
The demo program provides an edit box for entering expressions or creating/assigning variables. Another box displays the numeric result of the most recent evaluation. A list box displays the available, internally coded functions for reference. There is also a mini-disassembler which displays the generated evaluator code for immediate inspection. Examination of the disassembled code reveals the level of optimization attained by the parser/compiler.
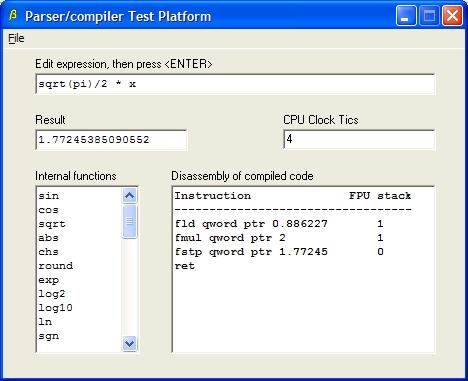
Screen Shot #1 of Demo Program
In the screen shot above, the variable, x, had been previously set to '2'. Note that the compiled code has reduced the entire coefficient expression to a single numeric value. The evaluator code, as shown in the disassembly, simply loads the constant, multiplies by the current value of x, and stores the result in a reference location.
A CPU clock tic counter is used to determine the number of actual processor clocks required to evaluate the expression. For a 1 GHz chip each tic represents 1 nanosecond. This feature uses the Pentium Time Stamp counter and is not available on other platforms.
In an application requiring multiple evaluations with arbitrary values of x the new values would be set prior to invoking the evaluator. It is difficult to imagine that any other run-time expression evaluation strategy could exhibit superior performance.
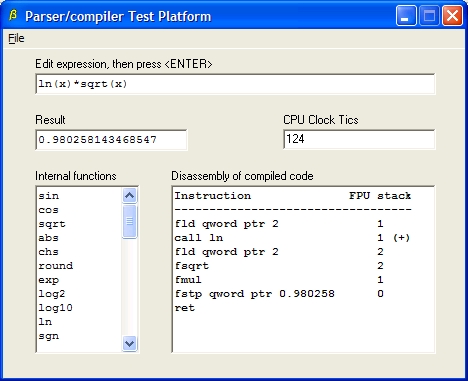
Screen Shot #2 of Demo Program
In the second example, shown above, x has also been set to '2'. Although it is not obvious from the simple disassembly, the internal function returning the natural logarithm of its argument is called without parameter pushes or stack frames. The argument is carried on the top of the FPU stack. Note that the square root is taken using an inline processor instruction so no function call overhead is required. For many expressions the only overhead penalty is the single call to the evaluator.
There are several additions and improvements required to elevate the status of the current code from proof of concept to beta release. First, robust error management needs to be put in place. Second, viable documentation needs to be completed. Third, constant folding related to user defined functions is not currently supported. As usual, a wish list of additional internal functions and operations will continue to grow.
The DLL and the demo program are intended to show some of the important features and properties of the method. They do not contain all of the features associated with finished applications, such as robust error management. Furthermore, some of the capabilities of the DLL are not used by the demo, including the ability to add user-defined functions and named constants. No help file is presently available, although the archive does include a small readme file. Borland C++ was used to create the DLL and the import library. Other platforms will require dynamic linking or the creation of a separate import library. See your compiler/linker documentation for particulars.
This software is offered as is. Use at your own risk. As the feature list expands and a viable help file is completed, updates will be posted.