
One of the most demanding applications in numerical analysis involves integration of functions. It is not uncommon for practical problems to involve integrands which are singular in the range of integration, or which must be integrated up to a singularity or out to infinity.
The contents of some of the navigation subsections above are:
In Numerical Analysis 101, students become acquainted with Simpson's rules, trapezoidal rules, and their variants to solve a limited class of integration problems with acceptable accuracy. More difficult problems which only yield to more powerful methods are deferred until the subjects of adaptive integration and Gaussian integration are discussed. In recent years, there has been growing interest in double exponential methods. In the following paragraphs, links to a variety of integrators are provided.
The state of the art in scientific software for solving a large class of problems is represented by Quadpack. This package was written in FORTRAN and you will find a complete port to C at QUADPACK. This C version is not a translation by a program which converts FORTRAN to C, but is a complete re-implementation of the package taking advantage of the dynamic memory support provided by C.
In this paper, I propose a new integration method which has the accuracy of Gauss-Legendre integration for the given number of function calls, but also provides a means to estimate the error of the integral. It is well suited to applications where function calls are expensive -- either as a stand alone, non-adaptive integrator, or as a preparation for a progressive method, such as Gauss-Patterson integration. The paper contains coefficients for the abscissae and weights for a number of integration orders computed to 60 digits.
Double exponential integration methods have become methods-of-choice in many mathematical applications and packages over the past few years. The flexibility, accuracy and efficiency are unmatched by any other general purpose integration strategy.
C source code for several double exponential integrators can be found here. C++ code for the integrators which support complex functions is here.
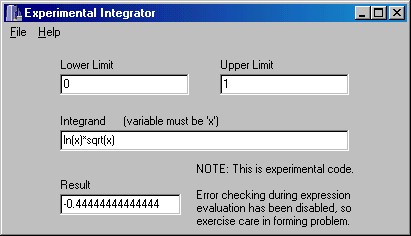
Screen Shot of Experimental Integrator
An experimental integrator, shown above, is available here. This integrator uses a shift-reduce parser to convert the expression for the integrand into a machine code representation (Intel x86) which is repeatedly called by an algorithm using the double exponential method (from Prof. Ooura, not from QUADPACK). The combination of techniques results in a very fast method which is robust in the presence of integrands with singular endpoints.
The integration problem solved in the screen shot above is challenging for several reasons. First, the function ln(x) is singular at zero and second, the function sqrt(x) has an infinite derivative there. This same problem is addressed in QUADPACK and solved with about 6 digit accuracy. Here the result is accurate to 14 digits.
This application was (and still is) intended to serve as a demonstration of a high performance expression evaluator. As such, it probably belongs in the parser section. Nevertheless, since it evaluates integrals there is some motivation for placing it here. (A coin toss assisted in the decision process.)